Simple Lens Approximations

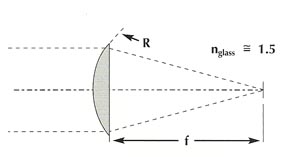For the plano-convex lens, the focal length equals twice the radius of the convex surface. This is also true for the plano-concave; howerver, since the radius is negative, this results in a negative focal length: f = 2R	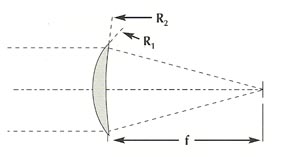For other forms of simple lenses, the following applies (Note: 0 = power): 1 EFL = 0 = 1 2 [ 1 R1 - 1 R2 ]
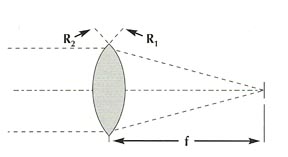For the double-convex or double-concave lens having equal radii, the focal length will equal the radius: R1 = R2 = f	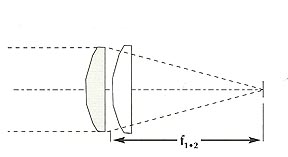If two or more thin lenses are stacked close together, their powers (1/EFL) may be added: 0(1+2) = 01 = 02 = f(1+2) = f1 * f2 f1 + f2
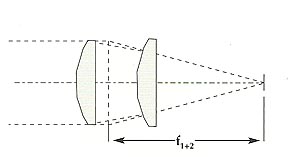If a substantial separation "d" exists between lenses, then: f(1+2) = f1 * f2 f1 + f2 -d